Содержание
Защита от вибрации
Определение
Вибрация - малые механические колебания, возникающие в упругих телах, в результате приложения внешней переменной силы. Когда говорят о вибрации, применительно к воздействию вибрации на человека, то подразумевают механические колебания частотой до 1000 Гц.
Классификация
- По способу передачи вибрации человеку.
- Общая вибрация - вибрация, которая передаётся человеку через опорные поверхности тела. Например, через ноги стоящего человека, таз сидящего человека и т.д.
- Локальная вибрация передаётся человеку через руки, ноги сидячего человека.
- По времени воздействия на человека.
- Постоянная - контролируемый параметр (виброскорость, виброускорение) изменяется менее чем в два раза или на 6 дБ.
- Непостоянная вибрация - величина нормируемых параметров изменяется в два раза (6 дБ) и более в течение рабочего дня.
Воздействие на человека
Вибрационные патологии по распространённости стоят на втором месте после пылевых (см. ссылку). Среди всего количества профессиональных заболеваний, каждый третий случай связан с воздействием на работников поышенных уровней вибрации и шума. Кроме того, наиболее высокая заболеваемость вибрационной болезнью регистрируется на предприятиях тяжелого, энергетического, транспортного машиностроения, угольной промышленности и цветной металлургии (см. ссылку).
- Общая вибрация воздействует в основном на вестибулярный аппарат, зрение. Особо необходимо отметить опасность возникновения резонанса колебаний внутренних органов и внешней вынуждающей силы, в результате чего может возникнуть реальная угроза повреждения внутренних органов.
Общая вибрация характерна для водителей грузовых автомобилей, трактористов, операторов тяжёлых станков, работников цехов по производству железобетонных конструкций и т.д.
- Локальная вибрация вызывает нарушение кровообращения, снижение тактильной, температурной и болевой чувствительности в конечностях. Возникают суставные деформации, развивается т.н. «вибрационная болезнь» (см. ссылку). Проявления вибрации, значительно усиливаются в охлаждающем микроклимате.
Характеристика вибрации
Согласно СН 2.2.4/2.1.8.566-96, гигиеническая оценка воздействия на человека постоянной и непостоянной вибрации должна производиться следующими методами:
- частотным (спектральным) анализом нормируемого параметра;
- интегральной оценкой по частоте нормируемого параметра;
- интегральной оценкой с учетом времени вибрационного воздействия по эквивалентному (по энергии) уровню нормируемого параметра;
Частотный анализ
В данном случае устанавливаются нормируемые диапазоны частот в виде октавных полос со следующими среднегеометрическими частотами:
- для общей вибрации - 1, 2; 4; 8; 16; 31,5; 63 Гц;
- для локальной вибрации - 8; 16; 31,5; 63; 125; 250; 500; 1000 Гц.
Нормируемыми параметрами являются среднеквадратичные значения виброскорости 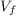 и виброускорения
и виброускорения 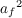 или их логарифмические уровни
или их логарифмические уровни 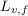 ,
, 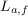 .
.
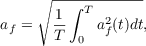
где
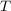 - длительность временного интервала, на котором производят усреднение.
- длительность временного интервала, на котором производят усреднение.
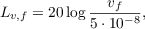
где
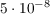 - опорное значение виброскорости,
- опорное значение виброскорости, 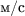 .
.
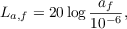
где
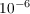 - опорное значение виброускорения,
- опорное значение виброускорения, 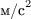 .
.
Интегральный анализ
При интегральной оценке по частоте нормируемым параметром является корректированное значение виброскорости 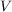 и виброускорения
и виброускорения  или их логарифмические уровни
или их логарифмические уровни 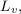 ,
, 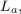 измеряемые с помощью корректирующих фильтров или вычисляемые по формулам:
измеряемые с помощью корректирующих фильтров или вычисляемые по формулам:
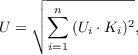
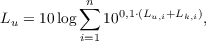
где 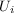 ,
, 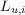 - среднееквадратичные значения виброскорости или виброускорения (их логарифмические уровни) в
- среднееквадратичные значения виброскорости или виброускорения (их логарифмические уровни) в  -ой частотной полосе;
-ой частотной полосе;  - число частотных полос в нормируемом частотном диапазоне;
- число частотных полос в нормируемом частотном диапазоне; 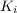 ,
, 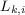 - весовые коэффициенты для
- весовые коэффициенты для  -ой частотной полосы соответственно для абсолютных значений или их логарифмических уровней, определяемые согласно СН 2.2.4/2.1.8.566-96.
-ой частотной полосы соответственно для абсолютных значений или их логарифмических уровней, определяемые согласно СН 2.2.4/2.1.8.566-96.
Интегральный анализ с учётом времени воздействия вибрации
При интегральной оценке вибрации с учетом времени ее воздействия нормируемым параметром является эквивалентное корректированное значение виброскорости или виброускорения 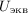 или их логарифмический уровень
или их логарифмический уровень 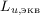 :
:
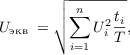
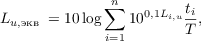
где 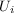 ,
, 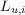 - корректированные по частоте значения и уровни контролируемого параметра виброскорости
- корректированные по частоте значения и уровни контролируемого параметра виброскорости 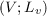 или виброускорения
или виброускорения 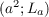 ;
; 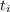 - время действия вибрации,
- время действия вибрации,  ;
; 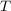 - общее время работы,
- общее время работы,  ;
;  - общее число интервалов действия вибрации.
- общее число интервалов действия вибрации.
Физические параметры колеблющейся системы
Для случая гармонических колебаний решение дифференциального уравнения вынужденных колебаний приводит к следующей связи физических параметров колеблющейся системы:
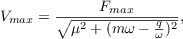
где 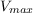 - максимальное значение мгновенной виброскорости,
- максимальное значение мгновенной виброскорости, 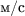 ;
;
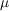 - коэффициент вязкого трения;
- коэффициент вязкого трения;
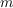 - масса колеблющейся системы,
- масса колеблющейся системы,  ;
;
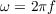 - циклическая частота, где
- циклическая частота, где 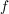 - частота колебаний,
- частота колебаний, 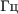 ;
;
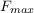 - максимальное значение вынуждающей силы,
- максимальное значение вынуждающей силы, 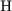 ;
;
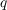 - жёсткость колеблющейся системы,
- жёсткость колеблющейся системы, 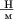 .
.
При этом для гармонических колебаний 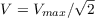 ,
,
где 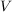 - среднеквадратичное значение виброскорости,
- среднеквадратичное значение виброскорости, 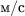 .
.
Кроме того, для гармонических колебаний связь между среднеквадратичными значениями виброскорости 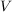 и виброускорения
и виброускорения  ,
, 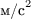 , выражется в виде
, выражется в виде 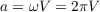 .
.
Методы защиты от вибрации
Организационные
- уменьшение времени воздействия;
- использование аналогичного инструмента с меньшим уровнем вибрации;
- использование СИЗ, например, рукавиц с вибродемпфирующими наладонниками;
- избегание охлаждающего микроклимата.
Лечебно-профилактические
- самомассаж конечностей, подвергшихся воздействию вибрации;
- общая гимнастика;
- физиотерапия (прогревание рук, ног в теплых ваннах);
- витаминотерапия (употребление витаминов группы B).
Технические меры
- уменьшение амплитуды вынуждающей силы;
- балансировка вращающихся элементов, например, роторов эл. двигателей и турбин, автомобильных колёс и т.д. Цель балансировки - совмещение центра тяжести тела с осью вращения. Метод не может дать точной балансировки.
- активная борьба с вибрацией. Применение сторонней системы, генерирующей колебания той же амплитуды и частоты, что и у колеблющейся системы, но противоположной фазы. Применяется на автономных установках (подводные лодки, корабли, баллистические ракеты).
- увеличение реактивного сопротивления системы
- увеличение массы;
- увеличение жёсткости системы.
- увеличение вязкого трения, например, обработка трубо- и воздухопроводов вибропоглащающими мастиками.